A Beautiful Graph
Last updated: 2025-03-28
I was messing around with inequalities, and I happened upon a simple expression with a very pleasing graph. That expression is
$$ \sin x < \sin y. $$
The graph of this inequality looks like:
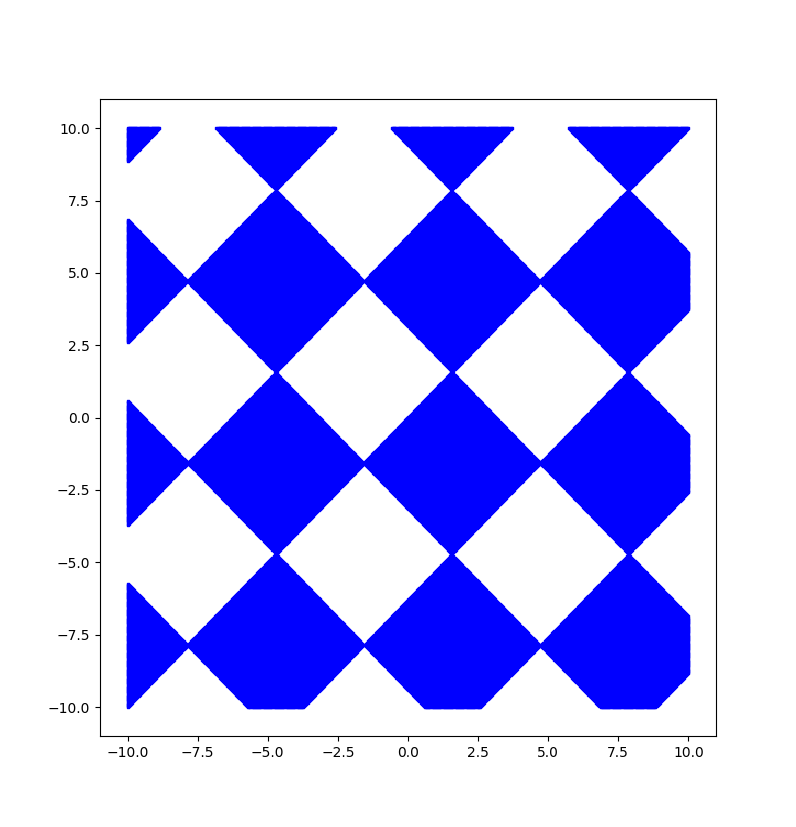
Let's explain this checkerboard pattern a little bit.
-
There's a set of lines with slope \( 1 \) spaced \( 2 \pi \) apart because
$$ \sin x = \sin \left( x + 2 \pi n \right), n \in \mathbb{Z}. $$
Hence, \( y = x + 2 \pi n \).
-
There's a set of lines of slope \( -1 \) spaced \( 2 \pi \) apart because
$$ \sin x = \sin \left( -x + \pi \cdot \left( 2 n - 1 \right) \right), n \in \mathbb{Z}. $$
Hence, \( y = -x + \pi \cdot \left( 2 n - 1 \right) \).
-
I'm pretty sure inequalities like this always alternate across lines of equality, but to see why the checkerboard pattern emerges in this particular inequality, consider the points \( (\pi/2, 0) \) and \( (-\pi/2, 0) \). For \( (\pi/2, 0) \), it's true that
$$ \sin(x) = 1 \ge 0 = \sin(y). $$
Thus, the region surrounding \( (\pi/2, 0) \) is not shaded. For \( (-\pi/2, 0) \), it's true that
$$ \sin(x) = -1 < 0 = \sin(y), $$
so the region surrounding \( (-\pi/2, 0) \) is shaded. Since the same will be true if we add or subtract \( 2 \pi \) either horizontally or vertically, it should be clear that square regions are alternately shaded and not shaded.